Kultaisen suhteen ymmärtäminen malleissa
Sanotaan, että luonnossa ja monissa ympärillämme on ”jumalallinen osuus”, joka löytyy kukista, mehiläispesistä, simpukankuorista ja jopa kehostamme.
Tämä jumalallinen osuus, joka tunnetaan myös nimellä kultainen suhde, jumalallinen suhde tai kultainen osa, voidaan soveltaa erilaisiin taiteisiin ja kuriin. Tiedemiehet väittävät, että mitä lähempänä kultaista leikkausta esine on, sitä enemmän ihmisaivot pitävät sitä miellyttävänä ja miellyttävänä.
Kauan tämän suhteen löytämisen jälkeen monet taiteilijat ja arkkitehdit ovat soveltaneet sitä teoksiinsa. Löydät kultaisen leikkauksen useista renessanssin mestariteoksista, arkkitehtuurista, maalauksista ja paljon muusta. Lopputulos: kaunis ja esteettisesti miellyttävä mestariteos.
Kukaan ei todellakaan tiedä, mikä kultaisessa leikkauksessa on, mikä miellyttää silmiämme. Useimmat olettavat, että se tosiasia, että se esiintyy kaikkialla ja on ”yleinen” osuus, saa meidät hyväksymään sen loogisena, harmonisena ja orgaanisena osuutena. Toisin sanoen se vain ”tuntuu” oikealta aivoillemme.
Joten, mikä on kultainen suhde?
Kultainen suhde, joka tunnetaan myös kreikaksi ”Phi”, on matemaattinen vakio. Se voidaan ilmaista yhtälöllä a/b=a+b/a= 1,618033987, jossa a on suurempi kuin b. Tämä voidaan selittää myös Fibonacci-sekvenssin, toisen jumalallisen sekvenssin, kautta. Fibonacci-sarja alkaa luvulla 1 (jotkut sanovat 0) ja laskee yhteen edellisen numeron saadakseen seuraavan (eli 1, 1, 2, 3, 5, 8, 13, 21…)
Jos yrität löytää kahden peräkkäisen Fibonacci-luvun osamäärän (eli 8/5 tai 5/3), tulos on hyvin lähellä kultaista suhdetta 1,6 eli φ(Phi).
Kultainen spiraali luodaan käyttämällä kultaista suorakulmiota. Kun sinulla on 1, 1, 2, 3, 5 ja 8 yksikön neliöruudut, kuten yllä olevassa kuvassa näkyy, voit aloittaa kultaisen suorakulmion rakentamisen. Käyttämällä neliön sivua säteenä sinun tulee luoda kaari, joka koskettaa neliön molempia pisteitä vinottain. Toista tämä jokaiselle kultaisen kolmion ruudulle, niin saat kultaisen spiraalin.
Missä voimme nähdä sen luonnossa:
Kultainen leikkaus ja Fibonacci-sekvenssi näkyvät kukkien terälehtien määrässä. Useimmilla kukilla on terälehtiä, jotka ovat joko kaksi, kolme, viisi tai useampia terälehtiä, jotka kaikki ovat osa jumalallista sekvenssiä. Esimerkiksi liljoilla on 3 terälehteä, leinikkikukassa 5, sikurikukassa 21 ja päivänkakkaralla 34. Ilmeisesti myös kukan siemenpää noudattaa kultaista suhdetta. Esimerkiksi auringonkukassa on siemenet, jotka ulottuvat keskeltä ja kasvavat sen ulkopuolella täyttämään siemenpään. Nämä on yleensä muodostettu kierteisiksi kuvioiksi, jotka muistuttavat kultaista spiraalia. Lisäksi siementen määrä yleensä laskee yhteen Fibonacci-luvut.
Kädet ja sormet noudattavat myös kultaista leikkausta. Katso lähempää! Kämmenen tyvestä sormenpäähän on erotettu osiin (luut). Yhden osan suhde seuraavaan on aina 1,618! Jopa kyynärvarren ja käden suhde on sama. Jopa varpaat ja kasvot, jatkamme ja jatkamme…
Sovellus taiteessa ja arkkitehtuurissa:
Kreikan Parthenonin väitetään rakennetun kultaisia mittasuhteita käyttäen. Porticon korkeuden, leveyden, pilarien, pilarin etäisyyden ja jopa koon mittasuhteiden uskotaan olevan suhteessa kultaiseen leikkaukseen. Se saattaa johtua siitä, että rakennus tuntuu suhteellisesti niin täydelliseltä ja se on aina ollut muinaisista ajoista lähtien.
Leonardo Di Vinci oli myös jumalallisen mittasuhteen (ja itse asiassa monien muiden mielenkiintoisten aiheiden) fani. Mona Lisan ihmeellinen kauneus saattaa johtua siitä, että hänen kasvonsa ja vartalonsa kunnioittavat kultaista suhdetta, samoin kuin todelliset ihmiskasvot luonnossa. Myös Leonardo Di Vincin Viimeinen ehtoollinen -maalauksen hahmot asettelevat hahmoja tavalla, joka käyttää kultaisia mittasuhteita. Kun rakennat kultaisia suorakulmioita kankaalle, keskiosuus asettaa Jeesuksen täydellisesti keskelle.
Logosuunnittelun sovellukset:
Ei niin yllättävää, että tämän jumalallisen annoksen käyttöä voidaan löytää myös monilla nykyajan tieteenaloilla, erityisesti suunnittelussa. Toistaiseksi keskitytään siihen, miten sitä voidaan käyttää logosuunnittelussa. Ensin tarkastellaan joitain maailman tunnetuimmista brändeistä, jotka ovat käyttäneet kultaista leikkausta logonsa parantamiseen.
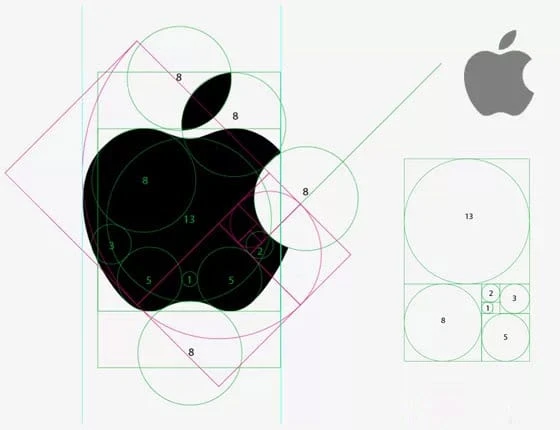
Ilmeisesti Apple on käyttänyt Fibonacci-sarjan mukaisia ympyröitä Apple-logon muotojen sijoittamiseen ja leikkaamiseen. Onko tämä tehty tahallaan vai ei, ei tiedetä. Lopputuloksena on kuitenkin selkeästi täydellinen ja visuaalisesti esteettinen logosuunnittelu.
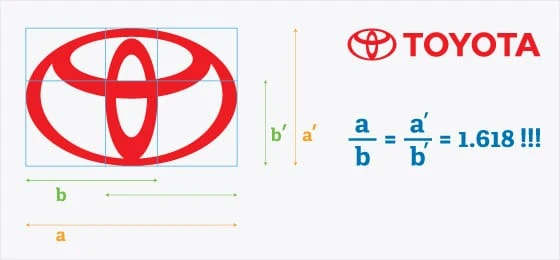
Toyotan logo noudattaa a- ja b-suhdetta muodostaen ruudukon, jossa on kolme rengasta. Huomaa, kuinka tämä logo käyttää suorakulmioita ympyröiden sijaan kultaisen leikkauksen luomiseen.
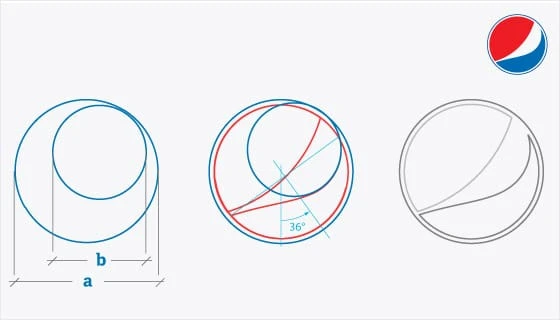
Pepsi-logo voidaan luoda kahdella risteävällä ympyrällä, joista toinen on suurempi kuin toinen. Suurempi verrattuna pienempään, kuten yllä olevassa kuvassa näkyy, on verrannollinen – arvasit sen! Heidän uusin litteä logonsa on yksinkertainen, tehokas ja kaunis!
Toyotan ja Applen lisäksi useiden muiden yritysten logojen, kuten BP:n, iCloudin, Twitterin ja Grupo Boticarion, uskotaan ottavan kultaisen leikkauksen huomioon. Ja me kaikki tiedämme kuinka kuuluisia nuo logot ovat – koska kuva ponnahtaa heti päähämme!
Näin voit käyttää sitä myös malleissasi
Piirrä kultainen suorakulmio yllä olevan kuvan mukaisesti keltaisella. Tämä voidaan tehdä rakentamalla neliöitä, joiden korkeus ja leveys on kultaiseen sarjaan kuuluva luku. Aloita ensimmäisestä yksiköstä ja aseta toinen 1 neliöosa sen viereen. Aseta toinen neliö, joka on 2 neliöyksikköä näiden kahden yläpuolelle. Sinulla on automaattisesti 3 yksikön puoli kolmen ensimmäisen ruudun kanssa. Kun olet rakentanut 3 yksikön neliön laatikon, päädyt 5 yksikön puolelle, josta voit tehdä toisen (5 yksikön neliön) laatikon. Tätä voi jatkua ikuisesti, ennen kuin huomaat, että sinulla on juuri tarvitsemasi koko!
Suorakulmio voidaan sijoittaa mihin tahansa suuntaan. Erottele pienemmät suorakulmiot ja koota niistä kutakin asettelu, joka toimii logosuunnittelusi ruudukkona.
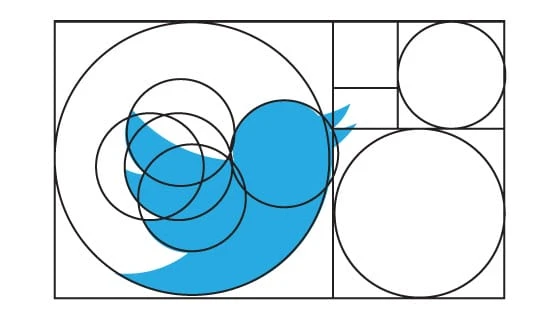
Jos logo on pyöreämpi, tarvitset pyöreän version kultaisesta suorakulmiosta. Voit tehdä tämän rakentamalla ympyröitä, jotka ovat verrannollisia Fibonacci-lukuihin. Luo kultainen suorakulmio käyttämällä vain ympyröitä (tämä tarkoittaa, että suurimman ympyrän halkaisija on 8, sitten pienemmän ympyrän halkaisija 5 ja niin edelleen). Erottele nyt nämä ympyrät ja aseta ne haluamallasi tavalla muodostaaksesi perusasettelun logosuunnittelullesi. Tässä esimerkki Twitter-logosta:
Huomautus: Sinun ei tarvitse käyttää kaikkia kultaisen suorakulmion ympyröitä tai suorakulmioita. Voit myös käyttää yhtä tiettyä kokoa toistuvasti.
Kuinka soveltaa sitä kuvioiden tekstiin:
Tämä on vähemmän hankalaa kuin logon suunnittelu. Yksinkertainen sääntö kultaisen leikkauksen soveltamiseen tekstissä on, että seuraava suurempi tai pienempi teksti on Phin mukainen. Katsotaanpa tätä esimerkkiä:
Jos fontin koko on 11, minulla on oltava alaotsikko, jossa on suurempi fontti. Kerron tekstin fontin kultaisella leikkauksella saadakseni suuremman luvun (11 1,6=17). Siksi alaotsikoni pitäisi olla kokoa 17. Nyt haluan vielä suuremman otsikon tai otsikon. Kerron alaotsikon kirjasimeni suhteella 27:ksi (17 1,6 = 27). Siinä se on! Tekstisi on nyt verrannollinen kultaiseen leikkaukseen.
Kuinka soveltaa sitä web-suunnitteluun:
Tässä menee vähän monimutkaisemmaksi. Voit pysyä uskollisena kultaiselle leikkaukselle jopa web-malleissasi. Jos olet kokenut web-suunnittelija, saatat jo arvata, missä ja miten tätä voidaan soveltaa. Kyllä, voimme tehokkaasti käyttää kultaista leikkausta ja soveltaa sitä verkkosivujemme ruudukkoihin ja käyttöliittymäasetteluihin.
Ota ruudukon kokonaispikselisi leveyden tai korkeuden mukaan ja käytä sitä kultaisen suorakulmion rakentamiseen. Jaa suurin leveys tai pituus, niin saat pienemmän luvun. Tämä voi olla pääsisältösi leveys tai korkeus. Jäljelle jää sivupalkki (tai alapalkki, jos olet käyttänyt sitä korkeudessa). Käytä nyt kultaista suorakulmiota soveltaaksesi sitä edelleen laatikoihisi, painikkeihisi, paneeleihisi, kuviisi ja tekstiisi. Voit myös rakentaa täyden ruudukon kultaisen suorakulmion pienempien versioiden perusteella, jotka on sijoitettu vaakasuoraan ja pystysuoraan, ja luoda pienempiä käyttöliittymäobjekteja, jotka ovat verrannollisia kultaiseen suorakulmioon. Voit käyttää tätä laskinta saadaksesi mittasuhteet .
Spiraali:
Voit myös käyttää kultaista spiraalia määrittääksesi, mihin sisältö sijoitetaan verkkosivustollasi. Jos kotisivusi on täynnä graafista sisältöä, kuten verkkokaupan verkkosivuilla tai valokuvausblogissa, voit hyödyntää kultaista kierremenetelmää, jota monet taiteilijat ovat käyttäneet teoksissaan. Ajatuksena on sijoittaa arvokkain sisältö spiraalin keskelle.
Sisällön klusterointi voidaan tehdä tavalla, joka seuraa kultaista suorakulmiota. Tämä tarkoittaa, että mitä enemmän keskiruutuja kohti spiraali liikkuu (yhden yksikön neliön laatikoita kohti), sitä ”tiheämmäksi” sisällöstä tulee.
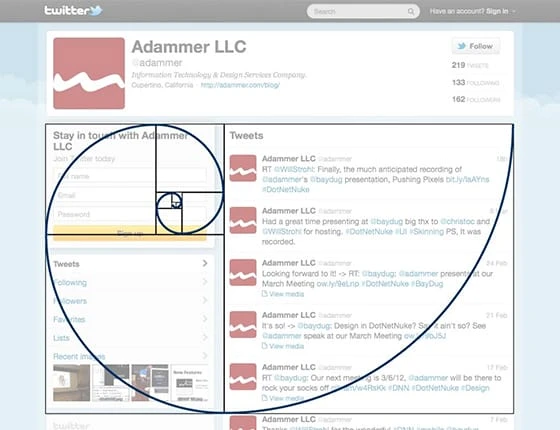
Tämän tekniikan avulla voit määrittää otsikon, kuvien, valikkorivin, työkalurivien, hakukenttien ja muiden elementtien sijainnin. Twitter on kuuluisa paitsi kultaisen suorakulmion käyttämisestä logosuunnittelussaan, myös sen käyttämisestä web-suunnittelussaan. Miten? Hyödyntämällä Kultaista suorakulmiota tai toisin sanoen kultaista spiraalikonseptia käyttäjiensä profiilisivulla.
Tätä ei ehkä ole helppo käyttää CMS-alustoilla, joissa sisällöntuottaja määrittää asettelun web-suunnittelijan sijaan. Kultainen suhde toimii hyvin WordPressin ja muiden blogityylisten mallien kanssa. Tämä johtuu luultavasti siitä, että sivupalkki on melkein aina läsnä blogisuunnittelussa, joka sopii hyvin kultaisen suorakulmion kanssa.
Helpompi tapa:
Hyvin usein suunnittelijat ohittavat monimutkaisen matematiikan ja soveltavat sitä, mitä he kutsuvat ” kolmassääntöksi ”. Tämä voidaan saavuttaa jakamalla alue kolmeen yhtä suureen osaan sekä vaaka- että pystysuunnassa. Tuloksena on yhdeksän yhtä suurta osaa. Viivan leikkauskohtaa voidaan käyttää muodon tai mallin polttopisteenä. Voit sijoittaa avainkohteen tai pääelementit yhteen tai kaikkiin näistä painopisteistä. Valokuvaajat käyttävät tätä käsitettä myös julisteissa.
Mitä lähempänä suorakulmiot ovat suhdetta 1:1,6, sitä näkyvämmin miellyttävä se on ihmisaivoille (koska se on lähempänä kultaista leikkausta).