Förstå det gyllene snittet i design
De säger att det finns en "gudomlig proportion" som vilar i naturen och många saker omkring oss. Du kan hitta den i blommor, bikupor, snäckskal och till och med vår kropp.
Denna gudomliga proportion, även känd som det gyllene snittet, det gudomliga snittet eller det gyllene snittet och kan appliceras på olika konster och discipliner. Forskare hävdar att ju närmare det gyllene snittet ett föremål är, desto mer tycker den mänskliga hjärnan att det är behagligt och behagligt.
Länge sedan detta förhållande upptäcktes har många konstnärer och arkitekter tillämpat det i sina verk. Du kan hitta det gyllene snittet i flera renässansmästerverk, arkitektur, målningar och mycket mer. Resultatet: ett vackert och estetiskt tilltalande mästerverk.
Ingen vet riktigt vad det är med det gyllene snittet som gläder våra ögon. De flesta antar att det faktum att det förekommer överallt och är en "universell" proportion är det som får oss att acceptera det som en logisk, harmonisk och organisk proportion. Med andra ord, det "känns" bara rätt för våra hjärnor.
Så, vad är det gyllene snittet?
Det gyllene snittet, även känt som "Phi" på grekiska, är en matematisk konstant. Det kan uttryckas med ekvationen a/b=a+b/a= 1,618033987, där a är större än b. Detta kan också förklaras genom Fibonacci-sekvensen, en annan gudomlig sekvens. Fibonacci-sekvensen börjar med 1 (vissa säger 0) och lägger ihop föregående nummer för att ge nästa (dvs. 1, 1, 2, 3, 5, 8, 13, 21…)
Om du försöker hitta kvoten för två efterföljande Fibonacci-tal (dvs. 8/5 eller 5/3), är resultatet mycket nära det gyllene snittet 1,6, eller φ(Phi).
Den gyllene spiralen skapas med hjälp av den gyllene rektangeln. När du har din rektangel med 1, 1, 2, 3, 5 respektive 8 enheter kvadratiska lådor, som visas i bilden ovan, kan du börja konstruera den gyllene rektangeln. Med hjälp av den kvadratiska sidan som din radie, ska du skapa en båge som vidrör båda punkterna på kvadraten diagonalt. Upprepa detta för varje ruta inom den gyllene triangeln och du kommer att få en gyllene spiral.
Där vi kan se det i naturen:
Det gyllene snittet och Fibonacci-sekvensen visas i kronbladsräkningen av blommor. De flesta blommor har kronblad som är antingen två, tre, fem eller fler kronblad som alla är en del av den gudomliga sekvensen. Till exempel har liljor 3 kronblad, smörblommor har 5, cikoriablomman har 21 och tusenskönan har 34. Tydligen följer fröhuvudet på en blomma också det gyllene snittet. Solrosen har till exempel ett frön som sträcker sig från mitten och växer runt utsidan för att fylla ut fröhuvudet. Dessa är vanligtvis formade i spiralmönster som liknar den gyllene spiralen. Vad mer är att fröantalet vanligtvis summerar till Fibonacci-talen.
Händerna och fingrarna följer också det gyllene snittet. Titta närmare! Handflatans bas till fingertoppen är separerad i delar (benen). Förhållandet mellan en del jämfört med nästa kommer alltid att vara 1,618! Även förhållandet mellan underarm och hand är detsamma. Till och med tårna och ansiktet, vi fortsätter och fortsätter…
Ansökan inom konst och arkitektur:
Parthenon i Grekland påstås ha byggts med de gyllene proportionerna. De dimensionella förhållandena för höjden, bredden, pelarna, kolumnavståndet och till och med storleken på portiken tros vara i förhållande till det gyllene snittet. Det beror möjligen på att byggnaden känns så proportionerligt perfekt och det har den alltid gjort sedan urminnes tider.
Leonardo Di Vinci var också ett fan av den gudomliga proportionen (och många andra nyfikna ämnen faktiskt!). Mona Lisas underbara skönhet kan bero på att hennes ansikte och kropp respekterar det gyllene snittet, liksom riktiga mänskliga ansikten i naturen. Dessutom arrangerar figurerna i målningen Sista Nattvarden av Leonardo Di Vinci figurer på ett sätt som använder de gyllene proportionerna. När du konstruerar gyllene rektanglar över duken, placerar mittproportionen Jesus perfekt i mitten.
Tillämpningar inom logotypdesign:
Inte så överraskande kan du också hitta användningen av denna gudomliga ranson i många discipliner i modern tid, särskilt design. Låt oss nu fokusera på hur det kan användas i logotypdesign. Låt oss först titta på några av världens mest kända varumärken som har använt det gyllene snittet för att perfekta sina logotyper.
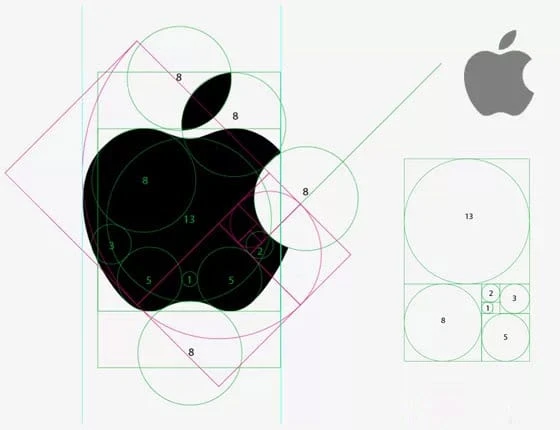
Uppenbarligen har Apple använt cirklar som är trogna Fibonacci-serien för att placera och klippa ut former av Apple-logotypen. Huruvida detta gjordes avsiktligt eller inte är okänt. Resultatet är dock helt klart en perfekt och visuellt estetisk logotypdesign.
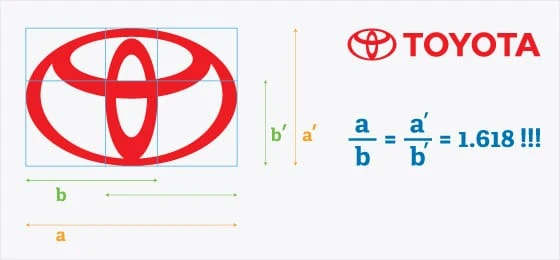
Toyotas logotyp följer förhållandet a och b för att bilda ett rutnät som lägger ut de tre ringarna. Lägg märke till hur den här logotypen använder rektanglar istället för cirklar för att skapa det gyllene snittet.
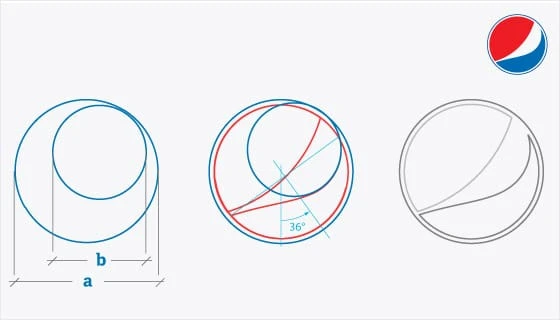
Pepsi-logotypen kan skapas av två korsande cirklar, en större än den andra. Den större jämfört med den mindre, som visas i bilden ovan, är proportionell mot — du gissade rätt! Deras senaste platta logotyp är enkel, effektiv och vacker!
Förutom Toyota och Apple tros flera andra företags logotyper som BP, iCloud, Twitter och Grupo Boticario ha tagit hänsyn till det gyllene snittet. Och vi vet alla hur kända dessa logotyper är – för en bild dyker genast upp i våra huvuden!
Så här kan du också använda det i dina mönster
Gör en skiss av den gyllene rektangeln som visas ovan i gult. Detta kan göras genom att konstruera rutor med höjder och bredder av ett tal som hör till den gyllene sekvensen. Börja med enhet ett och placera ytterligare 1 enhet i kvadrat bredvid den. Placera en annan ruta som är 2 enheter kvadrat ovanför de två. Du kommer automatiskt att ha en sida på 3 enheter med de tre första rutorna. Efter att ha konstruerat lådan med 3 enheter i kvadrat, kommer du att sluta med en 5 enheters sida från vilken du kan göra en annan (5 enheter kvadratisk) låda. Detta kan fortsätta i evigheter innan du inser att du har den exakta storleken du behöver!
Rektangeln kan placeras i vilken riktning som helst. Separera de mindre rektanglarna och använd var och en för att sätta ihop en layout som kommer att fungera som rutnätet för din logotypdesign.
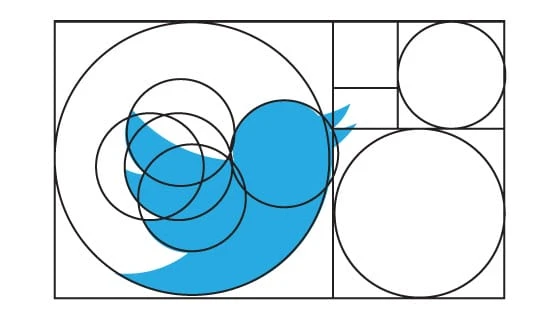
Om logotypen är mer cirkulär kommer du att behöva en cirkulär version av den gyllene rektangeln. Du kan göra detta genom att konstruera cirklar proportionella mot Fibonacci-talen. Skapa en gyllene rektangel med endast cirklar (detta betyder att den största cirkeln har en diameter på 8, sedan en mindre cirkel med diameter 5, och så vidare). Separera nu dessa cirklar och placera dem på vilket sätt du vill för att bilda en grundläggande layout för din logotypdesign. Här är Twitter-logotypen:
Obs: Du behöver inte använda alla cirklar eller rektanglar från den gyllene rektangeln. Du kan också använda en viss storlek upprepade gånger.
Så här applicerar du det på text på mönster:
Detta är mindre knepigt än att designa logotyper. Den enkla regeln för tillämpningen av det gyllene snittet i text är att nästa större eller mindre text ska vara enligt Phi. Låt oss titta på detta exempel:
Om mitt teckensnitts storlek är 11 måste jag ha en underrubrik som har ett större teckensnitt. Jag kommer att multiplicera mitt textteckensnitt med det gyllene snittet för att få fram ett tal som är större (11 1,6=17). Därför bör min underrubrik vara storlek 17. Nu vill jag ha en ännu större rubrik eller titel. Jag kommer att multiplicera min underrubrik typsnitt med förhållandet för att komma upp till 27 (17 1,6=27). Där har du det! Din text är nu proportionell mot det gyllene snittet.
Så här applicerar du det på webbdesign:
Här blir det lite mer komplicerat. Du kan vara trogen det gyllene snittet även i din webbdesign. Om du är en erfaren webbdesigner har du kanske redan gissat var och hur detta kan tillämpas. Ja, vi kan effektivt använda det gyllene snittet och tillämpa det på vår webbsidas rutnät och layouter för användargränssnitt.
Ta din totala rutnätspixel efter bredd eller höjd och använd det för att konstruera en gyllene rektangel. Dela den största bredden eller längden för att komma fram till ett mindre tal. Detta kan vara bredden eller höjden på ditt huvudinnehåll. Det du har kvar kan vara din sidostång (eller bottenstång om du har applicerat den på höjden). Fortsätt nu att använda den gyllene rektangeln för att ytterligare tillämpa den på dina rutor, knappar, paneler, bilder och text. Du kan också konstruera ett fullständigt rutnät baserat på mindre versioner av den gyllene rektangeln placerade horisontellt och vertikalt för att skapa mindre gränssnittsobjekt som är proportionella mot den gyllene rektangeln. För att få proportioner kan du använda den här kalkylatorn.
Spiralen:
Du kan också använda den gyllene spiralen för att bestämma var du ska placera innehållet på din webbplats. Om du har en hemsida laddad med grafiskt innehåll, till exempel på en webbshops hemsida eller en fotoblogg, kan du använda dig av den gyllene spiralmetoden som många konstnärer har använt i sina konstverk. Tanken är att placera det mest värdefulla innehållet i spiralens centrum.
Innehållsklustring kan göras på ett sätt som följer den gyllene rektangeln. Detta betyder att ju mer mot de mittersta rutorna spiralen rör sig (mot rutorna med en enhetsruta), desto "tätare" blir innehållet.
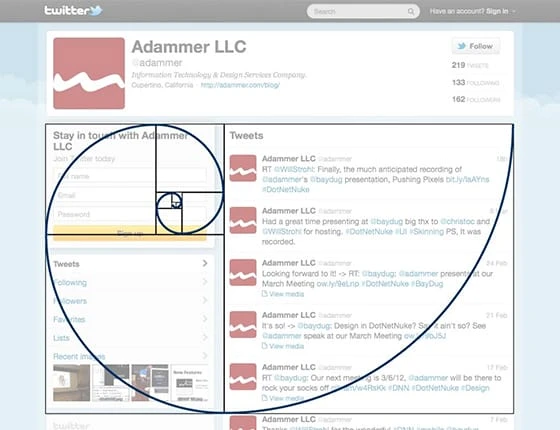
Du kan använda den här tekniken för att bestämma platsen för din rubrik, bilder, menyrad, verktygsfält, sökrutor och andra element. Twitter är känt för att inte bara använda den gyllene rektangeln i sin logotypdesign, utan också för att använda den för sin webbdesign. Hur? Genom att använda sig av den gyllene rektangeln, eller med andra ord det gyllene spiralkonceptet, på sina användares profilsida.
Detta kanske inte är lätt att använda på CMS-plattformar där innehållsskaparen bestämmer layouten istället för webbdesignern. Det gyllene snittet fungerar bra med WordPress och andra bloggdesigner. Detta beror förmodligen på att sidofältet nästan alltid finns på en bloggdesign som passar bra in i den gyllene rektangeln.
En enklare metod:
Mycket ofta hoppar designers över den komplexa matematiken och tillämpar vad de kallar " Rule of Thirds ". Detta kan uppnås genom att dela upp området i tre lika stora delar både horisontellt och vertikalt. Resultatet är nio lika delar. Linjeskärningen kan användas som en fokuspunkt för formen eller designen. Du kan placera ett nyckelämne eller dina huvudelement på en eller alla dessa fokuspunkter. Fotografer använder detta koncept till affischer också.
Ju närmare rektanglarna är förhållandet 1:1,6, desto mer synligt behagligt är det för den mänskliga hjärnan (eftersom det är närmare det gyllene snittet).