Forstå The Golden Ratio i design

De sier at det er en «guddommelig proporsjon» som hviler i naturen og mange ting rundt oss. Du kan finne den i blomster, bikuber, skjell og til og med kroppen vår.

Denne guddommelige andelen, også kjent som Golden ratio, Divine ratio, eller Golden section og kan brukes på ulike kunster og disipliner. Forskere hevder at jo nærmere det gylne snitt et objekt er, jo mer finner den menneskelige hjernen det behagelig og behagelig.

Lenge siden dette forholdet ble oppdaget, har mange kunstnere og arkitekter brukt det i verkene sine. Du kan finne det gyldne snitt i flere renessansemesterverk, arkitektur, malerier og mye mer. Resultatet: et vakkert og estetisk tiltalende mesterverk.

Ingen vet egentlig hva det er med det gylne snitt som gleder øynene våre. De fleste antar at det faktum at det vises overalt og er en «universell» proporsjon er det som får oss til å akseptere det som en logisk, harmonisk og organisk proporsjon. Med andre ord, det «føles» rett for hjernen vår.

Så, hva er det gylne snittet?

Det gyldne snitt, også kjent som «Phi» på gresk, er en matematisk konstant. Det kan uttrykkes med ligningen a/b=a+b/a= 1,618033987, der a er større enn b. Dette kan også forklares gjennom Fibonacci-sekvensen, en annen guddommelig sekvens. Fibonacci-sekvensen begynner med 1 (noen sier 0) og legger sammen forrige tall for å gi det neste (dvs. 1, 1, 2, 3, 5, 8, 13, 21…)

Hvis du prøver å finne kvotienten til to påfølgende Fibonacci-tall (dvs. 8/5 eller 5/3), er resultatet veldig nær det gylne snitt 1,6, eller φ(Phi).

Den gylne spiralen er laget ved hjelp av det gylne rektangelet. Når du har rektangelet ditt med henholdsvis 1, 1, 2, 3, 5 og 8 enheter kvadratiske bokser, som vist på bildet ovenfor, kan du begynne å konstruere det gylne rektangelet. Ved å bruke kvadratsiden som radius, skal du lage en bue som berører begge punktene på firkanten diagonalt. Gjenta dette for hver rute i den gylne trekanten, og du vil ende opp med en gylden spiral.

Hvor vi kan se det i naturen:

Det gylne snitt og Fibonacci-sekvensen vises i kronbladtellingen til blomster. De fleste blomster har kronblader som enten er to, tre, fem eller flere kronblader som alle er en del av den guddommelige sekvensen. For eksempel har liljer 3 kronblader, ranunkler har 5, sikoriblomsten har 21, og tusenfryden har 34. Tilsynelatende følger frøhodet til en blomst også det gylne snitt. Solsikken har for eksempel et frø som strekker seg fra midten og vokser rundt utsiden for å fylle ut frøhodet. Disse er vanligvis dannet i spiralmønstre som ligner den gylne spiralen. Hva mer er at frøtallet vanligvis summerer seg til Fibonacci-tallene.

Hendene og fingrene følger også det gylne snitt. Se nærmere! Basen av håndflaten til tuppen av fingeren er delt i porsjoner (beina). Forholdet mellom en del i forhold til den neste vil alltid være 1,618! Selv forholdet mellom underarm og hånd er det samme. Til og med tærne og ansiktet fortsetter vi og fortsetter…

Søknad innen kunst og arkitektur:

Parthenon i Hellas skal ha blitt bygget med de gylne proporsjonene. Dimensjonsforholdene til høyden, bredden, søylene, søyleavstanden og til og med størrelsen på portikken antas å være i forhold til det gylne snitt. Det er muligens fordi bygningen føles så forholdsmessig perfekt, og det har den alltid gjort siden antikken.

Leonardo Di Vinci var også en fan av den guddommelige proporsjonen (og mange andre nysgjerrige emner faktisk!). Den fantastiske skjønnheten til Mona Lisa kan skyldes det faktum at ansiktet og kroppen hennes respekterer det gylne snitt, og det samme gjør ekte menneskeansikter i naturen. Også figurene arrangert i Nattverd-maleriet av Leonardo Di Vinci arrangerer figurer på en måte som bruker de gylne proporsjonene. Når du konstruerer gylne rektangler på tvers av lerretet, plasserer midtproporsjonen Jesus perfekt midt i midten.

Applikasjoner i logodesign:

Ikke så overraskende kan du også finne bruk av denne guddommelige rasjonen i mange disipliner i moderne tid, spesielt design. For nå, la oss fokusere på hvordan det kan brukes i logodesign. La oss først se på noen av verdens mest kjente merker som har brukt det gylne snitt for å perfeksjonere logoene sine.

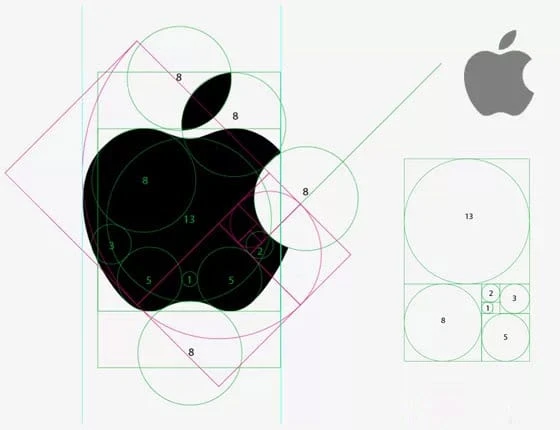
Tilsynelatende har Apple brukt sirkler som er tro mot Fibonacci-serien for å plassere og kutte ut former for Apple-logoen. Hvorvidt dette ble gjort med vilje eller ikke, er ukjent. Resultatet er imidlertid helt klart en perfekt og visuelt estetisk logodesign.

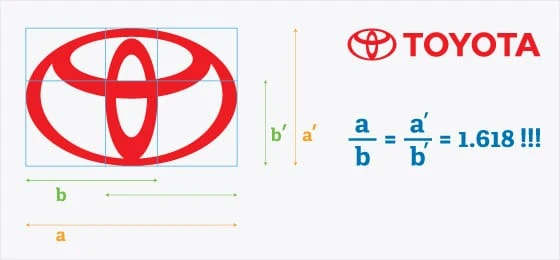
Toyotas logo følger a og b-forholdet for å danne et rutenett som legger ut de tre ringene. Legg merke til hvordan denne logoen bruker rektangler i stedet for sirkler for å lage det gylne snittet.

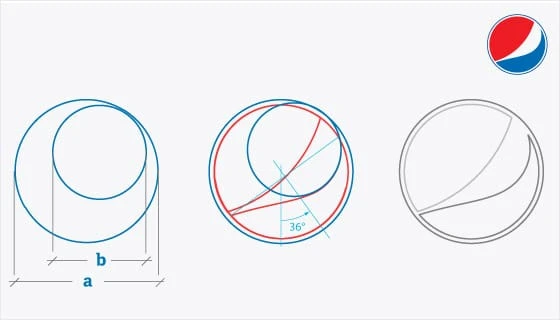
Pepsi-logoen kan lages av to kryssende sirkler, den ene større enn den andre. Den større sammenlignet med den mindre, som vist på bildet ovenfor, er proporsjonal med – du gjettet det! Deres nyeste flate logo er enkel, effektiv og vakker!

Bortsett fra Toyota og Apple, antas flere andre selskapers logoer som BP, iCloud, Twitter og Grupo Boticario å ha tatt det gylne snitt i betraktning. Og vi vet alle hvor kjente disse logoene er – for et bilde dukker umiddelbart opp i hodet vårt!

Her er hvordan du kan bruke det i designene dine også

Lag en skisse av det gylne rektangelet som vist ovenfor i gult. Dette kan gjøres ved å konstruere firkanter med høyder og bredder av et tall som tilhører den gylne rekkefølgen. Start med enhet en og plasser en annen 1 enhet kvadratisk brikke rett ved siden av. Plasser en annen firkant som er 2 enheter kvadrat over de to. Du vil automatisk ha en side på 3 enheter med de tre første rutene. Etter å ha konstruert boksen med 3 enheter i kvadrat, vil du ende opp med en 5 enheters side som du kan lage en annen (5 enheter kvadratisk) boks fra. Dette kan vare evig før du skjønner at du har akkurat den størrelsen du trenger!

Rektangelet kan plasseres i alle retninger. Skill de mindre rektanglene og bruk hver enkelt til å sette sammen et oppsett som vil fungere som logodesignets rutenett.

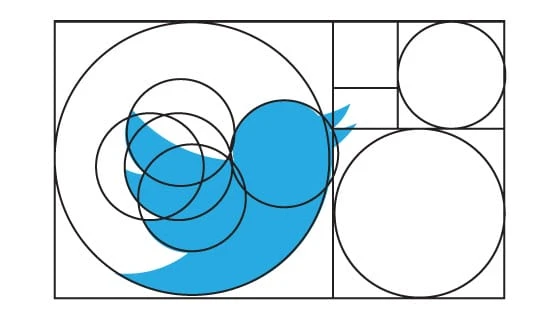
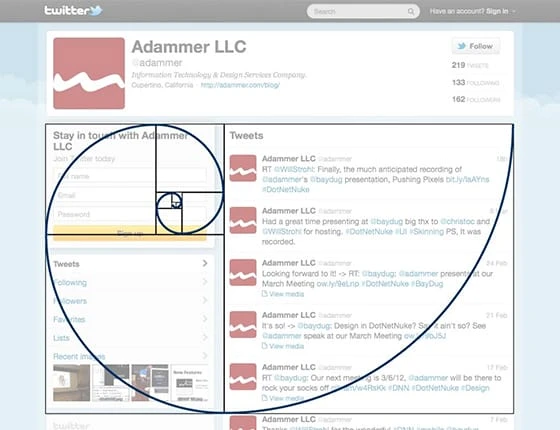
Hvis logoen er mer sirkulær, trenger du en sirkulær versjon av det gylne rektangelet. Du kan gjøre dette ved å konstruere sirkler proporsjonale med Fibonacci-tallene. Lag et gyllent rektangel med bare sirkler (dette betyr at den største sirkelen vil ha en diameter på 8, deretter en mindre sirkel med diameter 5, og så videre). Skil nå disse sirklene og plasser dem på hvilken som helst måte du vil for å danne en grunnleggende layout for logodesignet ditt. Her er eksempelet på Twitter-logoen:

Merk: Du trenger ikke å bruke alle sirklene eller rektanglene fra det gylne rektangelet. Du kan også bruke én bestemt størrelse gjentatte ganger.

Slik bruker du det på tekst på design:

Dette er mindre vanskelig enn logodesign. Den enkle regelen for bruk av det gylne snitt i tekst er at neste større eller mindre tekst skal være i henhold til Phi. La oss se på dette eksemplet:

Hvis skriftstørrelsen min er 11, må jeg ha en underoverskrift som har en større skrift. Jeg vil multiplisere tekstfonten min med det gylne snitt for å produsere et tall som er større (11 1,6=17). Derfor bør underoverskriften min være størrelse 17. Nå vil jeg ha en enda større overskrift eller tittel. Jeg vil multiplisere underoverskriften min med forholdet for å komme opp til 27 (17 1,6=27). Der har du det! Teksten din er nå proporsjonal med det gylne snitt.

Slik bruker du det på webdesign:

Her blir det litt mer komplisert. Du kan være tro mot det gylne snitt selv i webdesignene dine. Hvis du er en erfaren webdesigner, har du kanskje allerede gjettet hvor og hvordan dette kan brukes. Ja, vi kan effektivt bruke det gylne snitt og bruke det på nettsidens rutenett og brukergrensesnittoppsett.

Ta den totale rutenettpikselen din etter bredde eller høyde, og bruk den til å konstruere et gyldent rektangel. Del den største bredden eller lengden for å komme til et mindre tall. Dette kan være bredden eller høyden på hovedinnholdet ditt. Det du sitter igjen med kan være sidestangen din (eller bunnstangen hvis du har brukt den i høyden). Fortsett nå å bruke det gylne rektangelet for å bruke det ytterligere på boksene, knappene, panelene, bildene og teksten. Du kan også konstruere et komplett rutenett basert på mindre versjoner av det gylne rektangelet plassert horisontalt og vertikalt for å lage mindre grensesnittobjekter som er proporsjonale med det gylne rektangelet. For å få proporsjoner kan du bruke denne kalkulatoren.

Spiralen:

Du kan også bruke den gylne spiralen til å finne ut hvor du skal plassere innholdet på nettstedet ditt. Hvis du har en hjemmeside lastet med grafisk innhold, for eksempel på en nettbutikk-nettside eller en fotoblogg, kan du benytte deg av den gylne spiralmetoden som mange kunstnere har brukt i kunstverkene sine. Tanken er å plassere det mest verdifulle innholdet i sentrum av spiralen.

Innholdsgruppering kan gjøres på en måte som følger det gylne rektangelet. Dette betyr at jo mer mot de midtre rutene spiralen beveger seg (mot boksene med én enhet i kvadrat), jo «tettere» vil innholdet bli.

Du kan bruke denne teknikken til å bestemme plasseringen av overskriften, bildene, menylinjen, verktøylinjer, søkebokser og andre elementer. Twitter er kjent for ikke bare å bruke det gylne rektangelet i logodesignet, men også for å bruke det til webdesign. Hvordan? Ved å benytte seg av det gylne rektangelet, eller med andre ord det gylne spiralkonseptet, på brukernes profilside.

Dette er kanskje ikke lett å bruke på CMS-plattformer der innholdsskaperen bestemmer layouten i stedet for webdesigneren. Golden ratio fungerer godt med WordPress og andre bloggstiler. Dette er sannsynligvis fordi sidelinjen nesten alltid er til stede på et bloggdesign som passer godt inn i det gylne rektangelet.

En enklere metode:

Svært ofte hopper designere over den komplekse matematikken og bruker det de kaller » Rule of Thirds «. Dette kan oppnås ved å dele arealet i tre like deler både horisontalt og vertikalt. Resultatet er ni like deler. Linjekrysset kan brukes som et fokuspunkt for formen eller designet. Du kan plassere et nøkkelemne eller hovedelementene dine på ett eller alle disse fokuspunktene. Fotografer bruker dette konseptet til plakater også.

Jo nærmere rektanglene er forholdet 1:1,6, jo mer synlig er det for den menneskelige hjernen (siden det er nærmere det gylne snitt).